Introduction
The intense fragmentation of the Chelyabinsk meteoroid at altitudes of ~30–40 km resulted in <0.1% of the originally observed mass reaching the ground. Only tiny fragments were recovered near Chelyabinsk, with the largest fragment massing ~600 kg recovered from Lake Chebarkul (Borovička et al. 2013; Popova et al. 2013; Artemieva and Shuvalov 2016). The compressive strengths of the surviving meteorites were measured to be approximately 330 MPa (Popova et al. 2013). On the other hand, the apparent mechanical strength of the meteoroid during entry, determined from the dynamic pressure acting on the body while it fragmented (Borovička et al. 2013; Popova et al. 2013), was dramatically lower: It was estimated as 0.2 MPa during initial fragmentation at an altitude of ~83 km (Popova et al. 2013), and only as high as 1–5 MPa during intense fragmentation at altitudes of ~30–40 km. While the initial fragmentation of the meteoroid is easily attributed to internal weaknesses such as macroscopic cracks (Popova et al. 2013) or fractures (Borovička et al. 2013), we believe that the intense fragmentation that saw the survival of only small pieces may be accounted for by a previously unrecognized mechanism or process of air penetration into voids (cracks and pores) in the entering meteoroid.
Artemieva and Shuvalov (2001, 2016), Brown et al. (2013), and Shuvalov et al. (2016) recently studied the fragmentation of Chelyabinsk-sized meteoroids during atmospheric entry. Although aerodynamic pressures in the range from 0.1 to 10 MPa, leading to meteoroid breakup at the observed altitudes, were reported by these authors, none of these studies considered that the fragmentation of the meteoroid might be enhanced as a result of penetrating compressed air from the bow shock, even in cases where a multidimensional hydrodynamic code for interfacial flows (SOVA) (Shuvalov et al. 1999) was employed. While such codes do allow multiple materials to coexist in each computational cell, they do not properly simulate the exchange of energy and momentum that occur when one material percolates into another at the sub-mesh scale. We chose to study the interaction between the entering meteoroid and the atmospheric air using a multi-material computer code adapted from the Los Alamos code KFIX (Rivard and Torrey 1977). In this code, which is designed to simulate the interpenetration of two phases (a gas phase and solid phase in this case), the meteoritic material is treated as a porous granular solid while the atmospheric air is treated as a gas. Our simulations show that the penetration of air into the meteoroid from the high-pressure bow shock causes deformation and disruption that strongly enhances the fragmentation of the meteoroid mass. The process of fragmentation depends mainly on the porosity and permeability of the meteoroid, as well as its material strength, all of which we varied to understand their effects on the degree and manner of fragmentation. We show that the degree of air penetration influences the differing modes or styles of meteoroid fragmentation.
Previous work postulated several distinct modes by which an entering meteoroid might deform, a “pancake” type of deformation (Melosh 1981; Chyba et al. 1993; Ivanov et al. 1997; Bland and Artemieva 2003) and an explosive dispersion mode (Passey and Melosh 1980; Hills and Goda 1993; Artemieva and Shuvalov 1996), which may grade into one another as explosive dispersal follows an initial “pancake” expansion (Melosh 1981), as well as a mode in which a weak projectile might remain clumped into an aerodynamically shaped spike (Schultz et al. 2008), a mode that was postulated for the apparently unique Carancas impact. We show in the following that “pancake” or explosive dispersion modes are natural consequences of either high or low permeability to air penetration, respectively. Park and Brown (2012) considered percolation of liquid produced by ablation into a porous meteoroid, but did not recognize the role of the pressurized air itself.
The two unique aspects that we vary in our simulations are the porosity of the meteoroid and the rate of air penetration into its interior. As is known from modern astronomical studies of binary asteroids, the density of asteroids in space is surprisingly low (Scheeres et al. 2015), implying porosities of 20% or more. Such large porosities usually imply a correspondingly large permeability through cracks and voids in the body of the asteroid. This porosity, which characterizes the initial physical structure of the meteoroid, can be either microscopic, that is, below the scale of our code's resolution, or in the form of macroscopic voids that may occupy one or more computational cells. A recent paper (Robertson and Mathias 2017) examines the role of porosity on the strength and crushing of a meteoroid; however, their model does not allow air to actually infiltrate into the body of the meteoroid. Initially retaining only the near-vacuum of space at the starting altitude, the pore space controls the volume of air that may infiltrate into the body of the meteoroid. As the meteoroid descends into the atmosphere, pressure gradients drive the air into and through its body. In this work, we treat the porosity as a dynamic property that changes during the course of deformation of the meteoroid. The rate of air penetration is a function of the permeability, which enters into our code as a coupling parameter between the momentum of the solid and gas phases. It is derived from the physics of momentum transfer and, among other factors, is a strong function of the effective grain size as well as the porosity, as described in the next section. It thus also varies during the course of deformation of the meteoroid, increasing dramatically as the porosity increases.
In addition to crushing and dispersion, surface melting and ablation have long been recognized as an important process during meteorite entry (Bronshten 1983). The KFIX code is currently capable of modeling heat transfer between phases and can represent the melting and evaporation of silicates, as well as treating thermal radiation from and between the hot air and the solid meteoroid (Goldin and Melosh 2009). However, in this paper, we focus entirely on the novel process of air penetration into the body of the meteoroid because this is a previously unreported mechanism that we believe may be highly important during the entry of natural meteoroids, as opposed to engineered reentry vehicles in which this process is intentionally suppressed. Ablation probably plays a major role in evaporating the body of small asteroids, such as those at Chelyabinsk and Tunguska, after the main body of the meteoroid is dispersed and the resulting great increase in the surface area of the resulting small fragments enhances the likelihood of nearly complete evaporation of the mass. Indeed, of the total initial mass of the Chelyabinsk meteoroid of some 12,000 tons, only 4–6 tons were recovered in the form of solid meteorites (Popova et al. 2013). In the case of the more energetic 1908 Tunguska event, no fragments are known to have survived (Artemieva and Shuvalov 2016). Such enhanced evaporation is a fruitful avenue for future modeling; however, in this paper we concentrate entirely on the early phase of dispersion of the meteorite that then paves the way to more extensive ablation. We do not make any claim here to have modeled all aspects of the entry process, which will be a more major undertaking.
Several novel extensions to the KFIX code were required to explore the detailed interaction of air with an entering meteoroid. During entry the meteoroid begins at high altitude where the air is very rarefied, but it eventually reaches low altitudes where the air density is much higher. The enormous variation in density (over six orders of magnitude, plus the large differences in density between the meteoroid and surrounding air) is a challenge for any numerical code and it required internal modifications of KFIX to deal with this contrast. The most significant developments, which are described in the next section, include the description of the deformation of solid material as a function of an assumed effective viscosity (which simulates strength of the solid meteoroid by creating viscous deviatoric stresses that are relaxed when their second invariant reaches a yield surface, described in more detail below), the determination of deviatoric stresses in the meteoroid, and finally the implementation of the equations of motion in a reference frame that travels with the center of mass of the meteoroid. Model simulation results are then discussed, followed by conclusions in the last section.
Computational Model Development
KFIX is a two-dimensional (2-D), implicit Eulerian code that simultaneously solves the equations of motion of two interpenetrating fluids, both described as continua (Harlow and Amsden 1975a, 1975b; Rivard and Torrey 1977). Local flux conservation is enforced through the then-new staggered mesh method, which has by now become standard in most hydrodynamic codes (Patankar 1980). KFIX is derived from an older code, KACHINA (Amsden and Harlow 1974), which was later enhanced with the introduction of the fully implicit exchange (FIX) of mass, energy, and momentum among phases. Its solution algorithm is effective at all flow speeds between incompressible subsonic and hypersonic (Harlow and Amsden 1974). KFIX solves the equations describing the conservation of mass, momentum, and energy for each phase (including coupling of these quantities between phases) by enforcing the conservation of mass of each phase in each cell in the mesh through local adjustments of the pressure, meanwhile solving the equations of momentum conservation by an implicit scheme. The pressure in each cell is common to both fluids, although each fluid is given its own velocity, mass, density, and internal energy. Full energy conservation is imposed at the end of each cycle. This code, originally intended to model loss-of-coolant explosions in nuclear reactor cores, has subsequently been applied to model explosive volcanic eruptions (Valentine and Wohletz 1989) and the infall of impact ejecta following the Chicxulub impact (Goldin and Melosh 2009).
It is important to emphasize that KFIX treats its two phases (solid and gas in our case) as continua at all times. The solid phase, while representing a granular solid, is not actually composed of discrete particles in the code. The real “particles” in the body of the meteoroid (mineral grains or larger aggregations bounded by fractures) are generally below the resolution of the mesh and so KFIX represents them as a continuous fluid, an approximation similar to the way that conventional fluid dynamics approximates the ensemble of (much smaller!) atoms and molecules in a gas as continua. The code thus distinguishes a macroscopic density ρs′ for the solid or gas (averaged over many hypothetical particles in an individual computational cell) from a microscopic density ρs of an individual solid fragment (used in computing its equation of state [EOS]). These two densities are simply linked through the void ratio (or, equivalently, porosity) θ, where ρs′ = ρs (1 − θ). An analogous relation holds for the gas density, ρg′ = ρgθ. The granular aspect of the interaction between the gas and solid enters through the functions that regulate the exchange of momentum and energy between phases.
The principal link between the solid and gas phases in KFIX is through a parameter Kd that governs the exchange of momentum between the two phases. This parameter is a function of the void ratio, the relative velocity of the gas and solid, and a parameter r with dimensions of length. We use an analytical form suggested by Harlow and Amsden (1975b):
 (1)
(1)where μg is the dynamic viscosity of the gas, CD is a drag coefficient, which we take to be 1.7 for highly rarefied air, and the u values are the velocity vectors of the gas and solid, respectively. The first term in the curly brackets represents the Stokes flow viscous drag and the second is turbulent drag. The length parameter r is equal to the radius of a spherical particle in the limit of a very dilute solid for θ → 1, in which case the “solid” acts like a dilute dispersion of spherical droplets. However, in the opposite limit, θ → 0, this expression controls the permeability of gas in the solid. The equations of motion (Rivard and Torrey 1977) show that Kd is related to the standard Darcy permeability k through the simple relation:
 (2)
(2)The coefficient Kd is thus effectively an inverse permeability. In the limit of slow flow and small θ, this expression, with the above definition of Kd, reduces exactly to the permeability derived in equations 9 and 10 of Turcotte and Schubert (2002). The only difference is that r must now be interpreted as equal to about 1/7 of the spacing between pores (the variable b in Turcotte and Schubert's equation). When the flow speed increases, turbulent drag effectively decreases the permeability by increasing resistance to the air penetration. A similar variation of permeability with flow velocity has been observed experimentally (Chen et al. 2002).
All hydrodynamic codes require an EOS to complete the system of equations expressing conservation of mass, momentum, and energy. In general, this is a relation among the pressure P, density ρ, and temperature T or specific internal energy E for each material. KFIX differs from most hydrocodes, which demand a function P(ρ,E), in that it requires the density as a function of the internal energy and the pressure, ρ(P,E). Temperature is an accessory quantity derived from the internal energy through a heat capacity function.
We implement the EOS of air, ρ(P,T) = mP/(Z(P,T)RT), in which Z(P,T) is a compressibility factor and m is the mean molecular weight, over the possible range of atmospheric temperatures and pressures. Considering that complete breakup of the meteoroid may occur at altitudes as low as 20 km, with entry velocities ~15 km s−1, the dynamic pressure of air that interacts with the meteoroid can be as high as ~10 MPa. This pressure is an estimate of the air stagnation pressure Ps = 1/2ρgV2, where V is the flight velocity and tops the values of dynamic pressures determined during intense fragmentation of Chelyabinsk at altitudes of ~30–40 km. The air pressure thus ranges from a low of a few Pa at the beginning of entry up to a few MPa during intense fragmentation at lower altitudes. The air temperature correspondingly reaches a few thousand K in the bow shock. Under these conditions, air molecules may dissociate and the EOS becomes very complicated. The EOS of air is computed and tabulated for values of the compressibility factor Z(P,T) over the necessary range of temperatures and pressures in Hansen (1958), in linear intervals of temperature and in exponential intervals of the pressure, P = 10y, where y is an integer in the tables. We interpolate between tabulated values assuming a linear function for temperature and an exponential function for pressure. For nontabulated values in the required range of temperatures and pressures, Z(T,P) = Z(T,y) is determined by a Taylor approximation around the tabulated value Z(T0,y0):
 (3)
(3)In Hansen's tables, the compressibility factor Z is equal to 1 up to temperatures ~2000 K. The compressibility factor then rises slowly to Z = 2 for pressures ~0.1–10 MPa as temperatures approach 10,000 K, and only becomes higher than 2 for pressures that are below 1 MPa. Practically, however, the temperatures become higher than 2000 K only in the bow shock where aerodynamic pressures are highest, typically ranging from 0.01 to 10 MPa, and so the compressibility factor mostly varies between 1 and 2 in the bow shock.
We must also determine the heat capacity (at constant pressure) in addition to the density, because the conservation equations apply directly to the energy, not the temperature. However, most formulations of the EOS (including the one above) require temperature as an input, so it is essential to be able to convert internal energy into temperature. Hansen (1958) also tabulated the heat capacity Cp(P,T), which we interpolate from the tabulated values in an analogous manner to the compressibility. These tabulations give Z(P,T) and the heat capacity in terms of T, whereas the EOS ρ (P,E) requires the internal energy E as input. In practice, we converge on the correct value of T iteratively, as the EOS routine is called repeatedly during the normal operation of the code.
The meteoroid's material is modeled as a generic silicate (microscopic density ρ0 = 2170 kg m−3; this is lower than the full density of most meteorite components, but we use a lower value to account for isolated pores that do not contribute to the permeability), described by a “stiffened gas” EOS approximation (Harlow and Amsden 1971b; Lemons and Lund 1999) that includes both thermal and volume compression contributions to the pressure. This EOS is conventionally written in terms of density ρ as a function of pressure P and specific energy E below:
 (4)
(4)where a is the speed of sound, γ = Cp/Cv is the ratio of the specific heats, and the subscripts refer to thermodynamic conditions at P = 0, T = 300 K. For use in KFIX, this equation is solved algebraically for ρ(P,E). Given the high speed of sound in silicate rocks (a = 4 km s−1), the amount of compression is small even at 10 MPa and the thermal term seldom makes a significant contribution under conditions encountered in our simulations.
KFIX does not include an elastic or elastic-plastic constitutive model. Such constitutive models are readily implemented in Lagrangian codes, where the material remains in the same computational cell (Wilkins 1964); however, cell-to-cell fluxing of elastic strain becomes ambiguous in older Eulerian codes such as KFIX. Although modern Eulerian codes do successfully flux elastic strain, it is at the cost of considerable complexity. Instead, similar Eulerian codes implement a stress-dependent viscosity as a proxy for strength (Dienes and Walsh 1970). Viscous stresses are computed from the strain rates, which, unlike the elastic strains, are determined at each time step from the velocity gradients around each cell. The general idea is to impose an initial high viscosity that inhibits large deviatoric strains in the solid material until a stress yield criterion is exceeded, after which the viscosity is decreased rapidly to simulate fragmentation. As pressures and the accompanying deviatoric strains build up during atmospheric entry, the shear viscosity in the solid, μS, is maintained at a high value to prevent significant deformation. When the yield criterion is exceeded, the shear viscosity is lowered so that strain accumulates to simulate fragmentation. This “biviscous” approach was first initiated in the landslide literature (Dent and Lang 1983). The stress yield condition is attained when the magnitude of the second invariant of the deviatoric stresses exceeds an assigned yield stress of the meteoritic material, in accordance with a von Mises yield condition (a more rock-like Drucker–Prager yield condition that depends on pressure could also be implemented, but this difference played no role in our computations, as discussed below). The second invariant of the deviatoric stresses is calculated from the components of the stress tensor σij in axial symmetry:
 (5)
(5)When  exceeds the limiting value, the viscosity declines linearly to zero as a function of time after the criterion is exceeded, over an interval we chose to be 55 ms. We adopted a yield stress of 330 MPa, based on the crushing strength of recovered meteorites from the Chelyabinsk fall (Popova et al. 2013). We thus avoid the assumption of an ill-defined “effective strength” from the observed dynamic pressure at breakup and instead employ a value based on actual specimens of the meteoroid. In the results described below, this yield stress was, in fact, never exceeded. Instead, we attribute the disintegration of the Chelyabinsk meteoroid to loss of resistance to shear strain due to internal pressurization and the consequent loss of even frictional resistance as the rubbly matrix is expanded and the fragments lose contact with one another.
exceeds the limiting value, the viscosity declines linearly to zero as a function of time after the criterion is exceeded, over an interval we chose to be 55 ms. We adopted a yield stress of 330 MPa, based on the crushing strength of recovered meteorites from the Chelyabinsk fall (Popova et al. 2013). We thus avoid the assumption of an ill-defined “effective strength” from the observed dynamic pressure at breakup and instead employ a value based on actual specimens of the meteoroid. In the results described below, this yield stress was, in fact, never exceeded. Instead, we attribute the disintegration of the Chelyabinsk meteoroid to loss of resistance to shear strain due to internal pressurization and the consequent loss of even frictional resistance as the rubbly matrix is expanded and the fragments lose contact with one another.
In addition to this resistance to shear strain rate, the intrusion of pressurized air into the meteoroid matrix also exerts volume forces that tend to expand the enclosing solid following the gradient from high pressure at the leading edge to lower pressure at the meteoroid's periphery. This is an unconventional kind of deformation that can only arise in a two-phase system. Previous rock mechanical models (Johnson and Holmquist 1994) have incorporated complicated models for “bulking,” in which the two-phase system is implicitly solid rock and vacuum. However, this kind of deformation is a challenge for numerical modeling. KFIX takes these forces into account through a “bulk viscosity” that adds resisting forces to the stress tensor of the solid in response to the rate of increase or decrease in the macroscopic density ρS′ of the solid. Note that at the same time that the macroscopic density can impose tensional stresses to the solid matrix, the microscopic ρS density may be still be in compression, reflecting the intrusion of a pressurized gas phase into the matrix of the solid. The runs reported below did not include such a bulk viscosity (aside from a term that enforces the volume independence of the shear viscosity) because we assumed that our meteoroid was a “rubble pile” lacking tensional strength, but this may be incorporated in future simulations.
The effective shear strength of the meteoroid is also a strong function of the void fraction, or porosity. We again simulate an effective strength through a viscosity that is assumed to be a function of the void fraction (porosity). While it is well understood that pressurized pore water rapidly degrades the strength of porous rocks, pore gas can expand to a greater extent than water while maintaining high pressure, so this function must describe a broader range of dilation would be needed for a water-saturated rock. Current experimental data do not closely constrain this dependence, so we defined a well-behaved function to modulate the viscosity. This function remains close to 1 for moderate void fraction but falls rapidly as θ increases. The viscosity as a function of void fraction θ below the stress yield criterion is thus μ(θ) = μ0 f(θ), where μ0 is the viscosity of the nonporous bulk, and f(θ) is the modulating function:
 (6)
(6)The modulating function f(θ) is parameterized such that it decays to ~0.5 at θ = 0.5, then decays much faster at values of the void fraction greater than 0.7. The function is switched at θ = 0.7, given that rock with higher values of porosity seems unlikely to exhibit any significant strength.
An additional consideration is numerical stability when viscosity is present. The original developers of KFIX incorporated viscosity from the beginning and were able to define a stability criterion on the time step through a detailed analysis of higher order residuals of the implicit solution algorithm (Harlow and Amsden 1971a). They showed that when the viscosity is large, numerical stability requires a small time step. The maximum time step is thus calculated according to the criterion: δt < δy2/2ν, where δy is the cell size and ν is the kinematic viscosity, given by ν = μ/ρ in either phase. The overall stability is determined by the smallest time step in either phase for every cell in the mesh. We cannot therefore choose an arbitrarily large viscosity to limit deformation, but must choose a value that keeps deformation to a practical minimum while at the same time allowing a large enough time step to keep the run time reasonable (approximately a week per run in our case with a time step of 1 μs). The value that we generally used for a “large” viscosity is 105 Pa-sec, which is adequately large during the meteoroid's high altitude flight and becomes irrelevant once the object has become dispersed.
The equations of motion are implemented in the center-of-mass frame of the meteoroid to enable us to capture the motion of its entry over several kilometers, without using a computational mesh that will cover the entire range of flight. Our development of the equations of motion in a center-of-mass frame is similar to the formulation described by Li et al. (2002) in their derivation of the Navier–Stokes equation in a moving (accelerated) frame. In a center-of-mass frame with velocity  , the velocity relative to the center-of-mass frame is denoted as
, the velocity relative to the center-of-mass frame is denoted as  . The mass conservation equation, being a scalar, is invariant to the translation in velocity, and is described in the center-of-mass frame by:
. The mass conservation equation, being a scalar, is invariant to the translation in velocity, and is described in the center-of-mass frame by:
 (7)
(7)The acceleration of the center-of-mass frame must be added to the momentum conservation equation:
 (8)
(8)where the last term is the center-of-mass acceleration. Similar to the mass conservation equation, the energy conservation equation is a scalar (at nonrelativistic speeds) and does not require modification.
Atmospheric conditions vary enormously over the range of altitudes covered by the meteoroid entry, from highly rarefied at our initial altitude of 90 km to fragmentation at 20–30 km. The variation in pressure and temperature as a function of altitude h is determined through the barometric formula P(h) = P0 exp (−h/H), where P0 is the static atmospheric pressure at sea level and H is the atmospheric scale height, H = RT/gm, assumed to be isothermal for our purposes, T = 300 K, and g = 10 m s−2, for which g is the acceleration due to gravity, m is the molar mass of air, and R is the universal gas constant. We assume a linear flight path at constant angle to the horizon over a flat Earth, which is an adequate approximation for our primary focus, which is the dynamics of fragmentation and dispersion. The meteoroid enters the atmosphere at an angle α to the horizontal. The altitude of the meteoroid is determined as a result of the displacement along its flight path in Equation 9, where h0 is the initial altitude of entry,  is the total length of the flight path between entry and impact on the surface, and
is the total length of the flight path between entry and impact on the surface, and  is the displacement from the point of entry along the path of flight. The trajectory is displayed in Fig. 1a.
is the displacement from the point of entry along the path of flight. The trajectory is displayed in Fig. 1a.

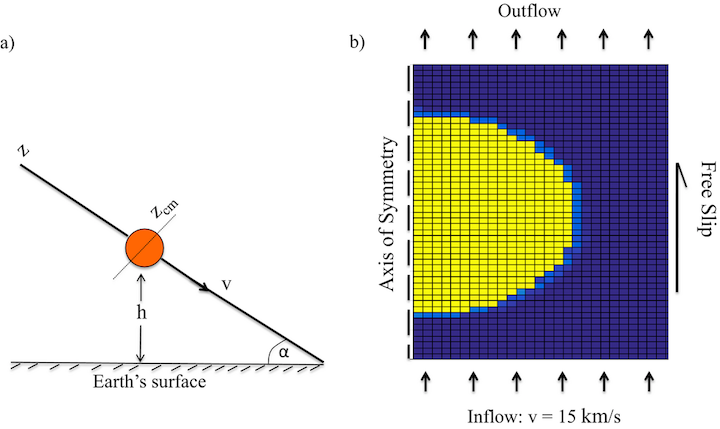
The computational mesh, which is centered on the meteoroid, is axially symmetric about its left edge. By imposing axial symmetry, the spatial three-dimensional (3-D) geometric description of the system is mapped into a 2-D representation. Each cell of the mesh is a rectangular toroid centered on the axis of symmetry, and the radius of the toroid is the horizontal distance of the cell from the axis of symmetry. The size of the mesh, 30 × 30 cells, while not large, is adequate to demonstrate the deformation and the breakup of the meteoroid into fragments. Assuming an entry speed of 15 km s−1, typical of many meteoroids including Chelyabinsk (~18 km s−1), in the center-of-mass frame, this implies an inflow of atmospheric air into the computational volume at a speed of 15 km s−1. The air inflow takes place through the bottom boundary of the computational mesh and its velocity changes proportionally to its deceleration to keep the center of mass approximately centered in the mesh. The density of the incoming air is adjusted to correspond to the altitude that the slowing meteoroid has attained at a given time. The air (and any solid fragments) flows out freely through the top boundary of the mesh, with a velocity that preserves continuity of the velocity gradient at the upper edge. The right edge of the mesh is a free-slip boundary at which the gradient in tangential velocities is zero. A diagram of the computational mesh with the described boundary conditions is sketched in Fig. 1b. The shear viscosity of the meteoroid is chosen to induce breakup of the meteoroid at altitudes similar to those at which intense fragmentation of the Chelyabinsk occurred. The time step of the simulation, which is chosen small enough to satisfy both with the viscosity criterion and the Courant flow condition, is 1 μs.
Model Simulations and Discussion
The entry modeling started at an altitude of 90 km, a height at which there was no observed fragmentation or brightness in thermal radiation for the Chelyabinsk fireball. The radius of the modeled meteoroid is 10 m or 20 cells per projectile radius, and the angle of entry is 45°. Results of the simulations can be visualized to display the profiles in the pressure buildup, the velocity of the air, the temperature of the air, and the density of the meteoroid scaled proportionately to the uncompressed bulk density. These physical quantities are displayed for the meteoroid at an altitude of 80 km in Fig. 2, which show that at this time, although the meteoroid is still mostly undeformed, a near-linear gradient in pressure has developed across the body of the meteoroid, from high pressure in the bow shock to near zero in the wake, as expected from elementary stress balance. The high temperatures in front of the meteoroid outline the bow shock and the somewhat lower temperatures indicate the shock in the wake. The steep angle of the shock cone is consistent with entry at the expected Mach 45, while air percolation is already seen to increase the porosity of the meteoroid along its leading edge.
More here: http://onlinelibrary.wiley.com/doi/10.1111/maps.13034/full
Quelle: WILEY
















